Jensen不等式以丹麦数学家约翰·詹森(Johan Jensen)命名。它给出均值的凸函数值和凸函数的均值间的大小关系。
if $X$ is a random variable and $\varphi$ is a convex function, then
$$
\varphi(E[X]) \le E[\varphi (X)].
$$
特别地,如果$\varphi$是严格凸函数,当且仅当$X$是常量时,上式取等号。Jensen不等式应用于凹函数时,不等号方向反向。
从凸函数说起, 设$\varphi$ 是定义域为实数的函数,如果对于所有的实数$x$,$\varphi(x)$的二次导数大于等于0,那么$\varphi(x)$是凸函数。如果$f(x)$的二次导数只大于0,不等于0,那么称 $\varphi(x)$ 是严格凸函数。当 $x$ 是向量时,如果$\varphi(x)$ 的 Hessian 矩阵H是半正定的,那么$\varphi(x)$是凸函数。如果 Hessian 矩阵H是正定的那么称$\varphi(x)$是严格凸函数。
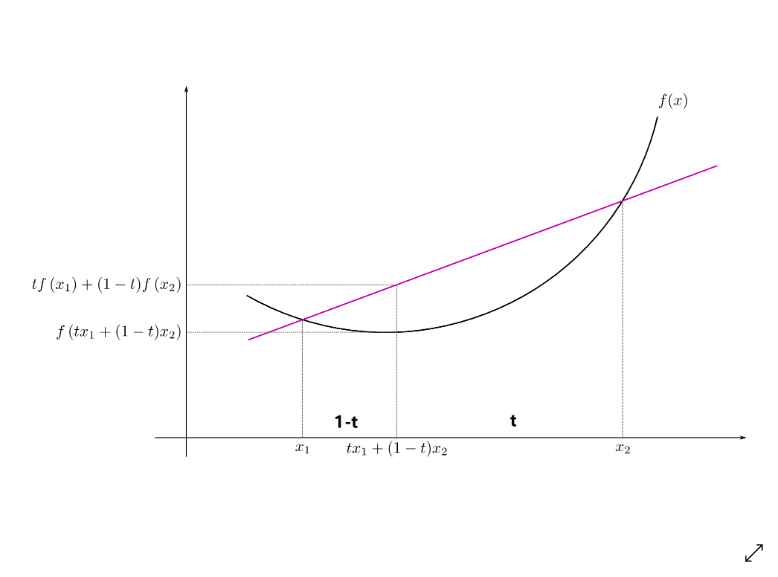
凸函数又如下性质: 过一个凸函数上任意两点所作割线, 割线一定在这两点间的函数图象的上方,即:
$$
f( tx_1 + (1-t)x_2)\leq tf(x_1)+(1-t)f(x_2). \tag{1}
$$
其中, $f$ 为如函数, 如下图所示:
将(1)推广到一般情形:
$$
f(\sum_{i=1}^n t_i x_i) \le \sum_{i=1}^n t_i f(x_i). \tag{2}
$$
其中: $x_i \in I, t_i \ge 0, \sum_{i=1}^n t_i =1, 1 \le i \le n$
令:
$$
t_i = \frac {p_i}{\sum_{i=1}^n p_i}.
$$
则 (2) 可以改写成
$$
f(\frac{\sum_{i=1}^n p_i x_i}{\sum_{i=1}^n p_i}) \le \frac{\sum_{i=1}^n p_i f(x_i)}{\sum_{i=1}^n p_i}. \tag{3}
$$
这就是jensen不等式的形式之一.
如果是$p_i$都取特殊的值,如:$p_i =1,i =1,2,\dots,n$ 则(3)可表示为
$$
f(\frac{\sum_{i=1}^n x_i}{n}) \le \frac{\sum_{i=1}^n f(x_i)}{n}
$$
即:
$$
f(E[X]) \le E[f(X)]. \tag{4}
$$
其中: $X=\{x_1, x_2, \dots, x_n\}$.
式(4)就是均值形式Jensen不等式.
reference