最大熵原理
在学习概率模型时, 所有可能的模型中熵最大的模型是最好的模型; 若概率模型需要满足一些约束, 则最大熵原理就是在满足已知约束的条件集合中选择熵最大模型. 最大熵原理指出, 对一个随机事件的概率分布进行预测时, 预测应当满足全部已知的约束, 而对未知的情况不要做任何主观假设. 在这种情况下, 概率分布最均匀, 预测的风险最小, 因此得到的概率分布的熵是最大. 要点为两个,即:
- 对于已知约束的情况下,建模要要满足约束;
- 除了约束外不做任何假设.
最大熵原理的实质就是, 在已知部分知识的前提下, 关于未知的分布最合理的推断就是符合已知知识最随机的推断.
看一个简单的例子: 设$a \in \{x, y\}$ 且 $b \in \{0, 1\}$, 要推断概率分布 $p(a,b)$. 现在我们唯一所知道的信息是 $p(x,0) + p(y,0) = 0.6$, 即:
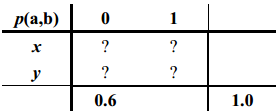
由于约束条件很少,满足条件的分布有无数多个,例如下面的分布就是满足已知条件的一个分布:
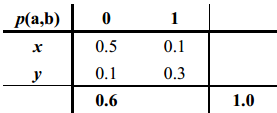
但按照最大熵原则,上述分布却不是一个好的分布,因为这个分布的熵不是满足条件的所有分布中熵最大的分布。按照最大熵的原则,应该选择的下面的分布:
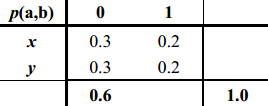
因为,最大熵原则要求,合理的分布应该同时满足要求:
$$
\begin {align}
& \hat p = \arg\max_{p \in P} H(p) = \arg\max_{p \in P} [- \sum_{a \in \{x, y\}, b \in \{0, 1\}} p(a, b) \log p(a, b)] \\
& p(x,0) + p(y,0) = 0.6 \\
& p(x,0) + p(y,0) + p(x,1) + p(y,1) = 1 \\
\end {align}
$$
最大熵模型
将最大熵原理应用于分类问题, 得到的就是最大熵模型.
为了下文论述方便, 此处先定义下文中需要使用的符号:
- $\mathcal {T} = \{(x_1, y_1),(x_2, y_2), \dots (x_N, y_N) \} $ 表示训练数据集
- $x_i \in \mathcal X$ 表示特征集合
- $y_i \in \mathcal Y$ 表示 label 集合
最大熵模型是用于处理分类问题的, 所以我们的最终目标是求 $p(y_i|x_i)$ .
按照最大熵的原理, 我们需要让模型满足已知的所有约束条件, 那么问题来了:
- 这些约束条件哪里来呢?
- 怎么表示这些约束?
特征函数
最大熵模型需要的约束实际上就是从训练数据$\mathcal T$中抽取的.
首先我们我们需要从训练数据中抽取岀了若干特征. 其次使用 特征函数 来表示这些特征. 对于一个给定的样本 $(x,y)$ ,特征函数可以定义为任意实值函数, 通常我们都是使用二值函数来定义. 如下所示:
$$
f(x, y) =
\left \{
\begin {align}
1, & x, y满足条件\\
0, & otherwise
\end {align}
\right .
$$
下面使用词性标注的例子来说明:
假设我们需要判断”打”字是动词还是量词,已知的训练数据有:
(x_1,y_1)=(一打火柴,量词)
(x_2,y_2)=(三打啤酒,量词)
(x_3,y_3)=(五打塑料袋,量词)
(x_4,y_4)=(打电话,动词)
(x_5,y_5)=(打篮球,动词)
通过观察, 我们发现, “打”前面为数字时, “打”是量词, “打”后面为名词时, “打”是动词,这就是从训练数据中提取的两个特征, 可分别用特征函数表示为:
$$
f(x, y) =
\left \{
\begin {align}
1, & “打”前面为数字 \\
0, & otherwise
\end {align}
\right .
$$
$$
f(x, y) =
\left \{
\begin {align}
1, & “打”前面为名词 \\
0, & otherwise
\end {align}
\right .
$$
对于上面的5条训练数据,我们便有:
$$
f_1(x_1, y_1) = f_1(x_2, y_2)=f_1(x_3,y_3)=1; f1(x_4, y_4)=f1(x_5, y_5)=0 \\
f_2(x_1, y_1) = f_2(x_2, y_2)=f_2(x_3,y_3)=0; f2(x_4, y_4)=f2(x_5, y_5)=1 \\
$$
经验分布与预测分布
所谓经验(概率)分布是指在训练数据$\mathcal T$进行统计得到的分布,用 $\tilde p$ 表示. 由于真实分布是无法直接获取的(如果内得到,我们就不需要训练模型了), 通常我们都是使用经验分布来表示真实分布(要求: 训练数据集是从总体中 独立同分布 抽样获取的).
在最大熵模型中, 需要考察两个经验分布 $\tilde p(x,y)$ 和 $\tilde p(x)$,其定义分别为:
$$
\begin {align}
& \tilde p(x, y) &= \frac {cout(x, y)}{N} \\
& \tilde p(x) &= \frac {cout(x)}{N} \\
\end {align}
$$
其中, $count(x,y)$ 和 $cont(x)$ 分别表示 $(x,y)$ 和 $x$ 在训练数据 $mathcal T$ 中出现的次数.
同时存在一个模型(即我们最终训练得到的模型, 目前未知), 该模型也可以预测 $p(y|x)$. 那么利用Beyes定理 $(x, y)$ 的预测分布可以表示为:
$$
p(x, y) = p(x) p(y| x)
$$
但是上式中的 $p(x)$ 是未知的. 此处使用 $\tilde p(x)$ 来对 $p(x)$ 进行近似, 那么 $(x, y)$ 的预测分布可以近似为:
$$
p(x, y) \approx \tilde p(x) p(y| x)
$$
利用上述定义的特征函数, 经验分布和预测分布,就可以进一步定义我们所需的约束条件了.
约束条件
在最大上模型中, 建立约束条件的基础是我们认为:
每一个特征对应的特征函数 $f$, 在 $\mathcal T$ 上关于经验分布 $\tilde p(x,y)$ 的数学期望 $E_{\tilde p}(f)$ 与它们在模型中关于 $p(x,y)$ 的数学期 $E_p(f)$ 望相等.
$$
\begin {align}
E_{\tilde p}(f) & = \sum_{(x,y) \in \mathcal T} \tilde p(x, y)f(x, y) \\
E_p(f) & = \sum_{(x,y) \in \mathcal T} p(x, y)f(x, y) \\
& = \sum_{(x,y) \in \mathcal T} \tilde p(x) p(y \mid x)f(x, y) \\
\end {align}
$$
即:
$$
\begin {align}
& E_{\tilde p}(f) = E_p(f) \\
\\
& \sum_{(x,y) \in \mathcal T} \tilde p(x, y)f(x, y) = \sum_{(x,y) \in \mathcal T} \tilde p(x) p(y \mid x)f(x, y) \\
\end {align}
$$
假设从训练数据中抽取了 $n$ 个特征, 便有 $n$ 个特征函数 $f_i, (i=1, 2, \dots, n)$, 相应的就有 $n$ 个约束条件.
$$
E_{\tilde p}(f_i) = E_p(f_i), (i=1, 2, \dots, n)
$$
模型表示
给定训练数据 $\mathcal T$, 我们的目标是:利用最大熵原理选择一个最好的分类模型, 即对于任意给定的输入 $x \in \mathcal X$,可以以概率 $p(y \mid x)$ 输出 $y \in \mathcal Y$.
最大熵模型本质上是一个约束最优化问题,即在给定的约束下求目标函数的最值问题。 上面已经介绍了约束条件,基于最大熵原理我们的目标函数即为熵的最大化,即:
$$
\begin {align}
H(p) = H(y \mid x) & = -\sum_{(x,y) \in \mathcal T} p(x, y) \log p(y \mid x) \\
& = -\sum_{(x,y) \in \mathcal T} p(x) p(y \mid x) \log p(y \mid x) \\
& = -\sum_{(x,y) \in \mathcal T} \tilde p(x) p(y \mid x) \log p(y \mid x) \\
\end {align}
$$
由于 $p(x)$ 是未知的. 此处使用 $\tilde p(x)$ 来对 $p(x)$ 进行近似。
对综上给出形式化的最大熵模型:
对于给定的训练数据$\mathcal T$, 特征函数 $f_i(x,y), i=1,2,…,n$, 最大熵模型就是求解:
$$
\begin {align}
\max_p & H(p) & = -\sum_{(x,y) \in \mathcal T} \tilde p(x) p(y \mid x) \log p(y \mid x) \\
s.t. & & E_{\tilde p}(f_i) = E_p(f_i), (i=1, 2, \dots, n) \\
& & \sum_y p(y \mid x) = 1 \\
\end {align}
$$
其中的条件 $\sum_y p(y \mid x)=1$ 是为了保证 $p(y \mid x)$ 是一个合法的概率分布.