PRank算法

Posted on | In

LTR模型可以分为 point-wise、pair-wise、list-wise三类，Prank算法属于point-wise模型。

Pointwise可以用于推荐系统中也可以用于IR中。

以Pointwise在IR中的应用为例，它处理对象是doc-query pair，将doc-query的match信息转化为特征向量后，机器学习系统根据训练得出的模型对doc-query pair进行打分，打分的顺序即为搜索排序的结果。计算打分的公式如下：

$$
\mathrm{score} = \mathbf w \cdot \mathbf x
$$

其中$\mathbf w$为特征各维度的权重，$\mathbf x$为doc-query match信息转化为的特征向量。

在Ranking问题中我们使用的训练样本的label值不是分数，而是一个具有强弱分级的label，如Perfect > Excellent > Good > Fair > Bad 这样具有强弱关系的五级label。为了将score映射到分级label，需要设置5个阈值来区分score的label。如果score落在某两个相邻阈值之间，则划分为相应的label，常见算法包括：PRank、McRank。如下图所示为PRank算法示意图：

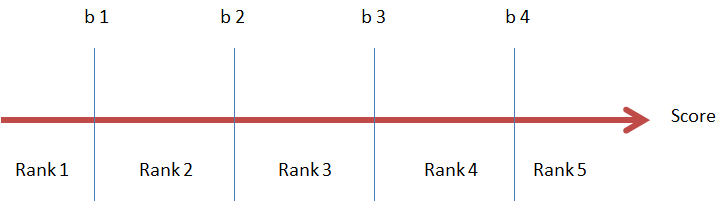
算法思想

数据：$X_{T \times n}$ ， $y， y \in {1, 2, 3, \dots, k}$， 即训练样本量为$T$， 特征维度为n，$y$共有k个等级的取值。

PRank的目标是训练一个ranking rule H : $R^n \rightarrow y$ ，即，将样本特征投影到$k$个等级上。$H$ 定义如下：
$$
H(\mathbf x)=\min_{r \in {1, 2, 3, \dots, k}}\{r: \mathbf w \cdot \mathbf x - b_r < 0 \}
$$
其中：$\mathbf w$ 和 $b_r, r \in {1, 2, 3, \dots, k}$ 是模型参数。 $ \mathbf w \cdot \mathbf x$ 就是上文中所说的score，$k$ 个 $b_r$ 就是上文所说的阈值，$b_1 \le \dots \le b_{k-1} \le b_k = \infty$ 。如上文所述如果一个样本满足$b_{r-1} \lt \mathbf w \cdot \mathbf x \le b_r$ ，则该样本的预测rank值为$r$，即，$\hat y = H(\mathbf x) = r$。

模型参数估计

PRank模型存在两组参数$\mathbf w$ 和 $b_r, r \in {1, 2, 3, \dots, k}$ ，只要能将这两组参数确定下来，就大功告成。下面讲解参数的确定过程。PRank更新参数的方法类似于随机梯度下降法，即，每当预测错误一个样本后，就更新参数。

对于一个样本$(\mathbf x, y)$ 和模型参数$\mathbf w$ 和 $b_r, r \in \{1, 2, 3, \dots, k\}$ 。如果模型能够正确预测，则 :
$$
\begin {align}
& \mathbf w \cdot \mathbf x \gt b_r , r \le y-1 \\
& \mathbf w \cdot \mathbf x \lt b_r , r \ge y
\end {align}
$$

如上所述，$y$的取值是从集合$\{1, 2, 3, \dots, k\}$ 中选取。模型引入辅助变量$s$(原文中依然使用$y$，我认为可能产生符号混淆，所以改用$s$) ，

$s$是一个向量，长度为$k-1$ ， $s$ 与 $y$ 是一一对应的(类似于多分类问题中，使用onehot编码将label向量化)。对于样本 $(\mathbf x, y)$来说，s的各维度值定义如下：
$$
\begin {align}
& s_r = +1 , r \le y-1 \\
& s_r = -1, r \ge y , r \lt k
\end {align}
$$
例如当 $k=5$时，$y$的取值与$s$的关系如下：

$$
\begin {align}
& y=1 \Leftrightarrow s=[-1, -1, -1, -1] \\
& y=2 \Leftrightarrow s=[ +1, -1, -1, -1] \\
& y=3 \Leftrightarrow s=[ +1,+1, -1, -1] \\
& y=4 \Leftrightarrow s=[ +1,+1,+1, -1] \\
& y=5 \Leftrightarrow s=[ +1,+1,+1,+1]
\end {align}
$$

对于样本$(\mathbf x, y)$来说， 对于所有的$r \in \{1, \dots , k-1\}$ ：

  1. 如果模型预测结果是正确的，则$s_r\cdot (\mathbf w \cdot \mathbf x - b_r ) \gt 0$，此时参数不需要更新
  2. 如果模型预测结果是错误的，则存在$s_r\cdot (\mathbf w \cdot \mathbf x - b_r ) \le 0$，此时需要更新参数

对于特定的$r$，如果$s_r\cdot (\mathbf w \cdot \mathbf x - b_r ) \le 0$， 则说明score值$\mathbf w \cdot \mathbf x$ 落在了阈值$b_r$的错误的一侧，为了改正这个错误的预测，只需要将$\mathbf w \cdot \mathbf x$和$b_r$相对移动就能完成对于参数$\mathbf w$ 和 $b_r$ 的更新。更新公式如下：

对于$s_r\cdot (\mathbf w \cdot \mathbf x - b_r ) \le 0$：
$$
\begin {align}
& b_r = b_r - s_r \\
& \mathbf w = \mathbf w + s_r \cdot \mathbf x
\end {align}
$$
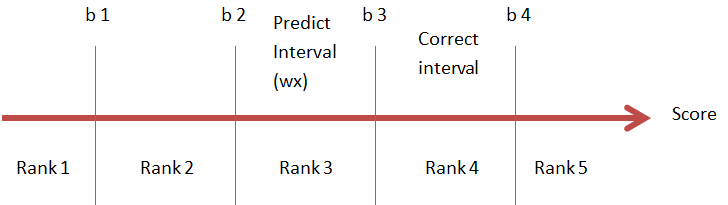
当$y=4$ ，预测值落在了Rank 3 范围内时：$s_ 3= +1$ ，此时需要将$b_3$向左移动， $\mathbf w \cdot \mathbf x$向右移动。
$$
\begin {align}
& b_3 = b3 - s_3 = b3 - (+1) \\
& \mathbf w = \mathbf w + (+1) \cdot \mathbf x \Leftrightarrow \mathbf w \cdot \mathbf x = \mathbf w \cdot \mathbf x + (+1) \mathbf x^2
\end {align}
$$

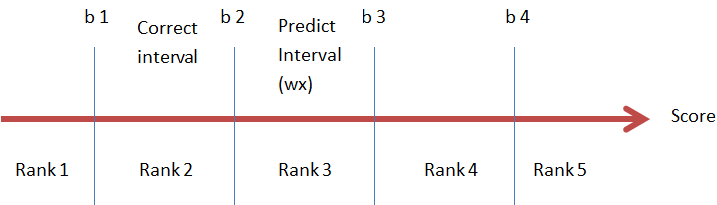
当$y=2$ ，预测值落在了Rank 3 范围内时：$s_ 2= -1$ ，此时需要将$b_2$向右移动， $\mathbf w \cdot \mathbf x$向左移动。
$$
\begin {align}
& b_2 = b2 - s_2 = b3 - (-1) \\
& \mathbf w = \mathbf w + (-1) \cdot \mathbf x \Leftrightarrow \mathbf w \cdot \mathbf x = \mathbf w \cdot \mathbf x + (-1) \mathbf x^2
\end {align}
$$

如果有存在多个$r$ 使得$s_r\cdot (\mathbf w \cdot \mathbf x - b_r ) \le 0$时，更新过程如下图所示：

实现流程

PRank算法比较简单，基本流程如下所示：

实现代码

以下为PRank算法的Python实现代码

note：由于实际环境中我们使用的rate是从0开始的，如5级使用的是$\{0, 1, 2, 3 ,4\}$ 来做标记，所以下面的代码和上文中的论述有一点出入。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import numpy as np

def prank(X, y, rate_levels, epochs=10, delta=0.01):
    '''
    epochs: int, 收敛之前 遍历样本次数
    rate_lavels: int, y中rate的级别数量，如y用 0,1,2,3 标记，则rate_lavels = 4
    X: 训练样本feature集合
    y: 训练样本的rate集合，需要从 0开始。如果未5级标注，需要为 0, 1, 2, 3, 4
    delta: float, 终止迭代条件
    '''
    N = len(X)  # 样本量
    D = len(X[0])  # 样本维度
    theta = np.zeros(D)
    b = np.zeros(rate_levels - 1)
    s = np.zeros((N, rate_levels - 1))  # 辅助变量，类似于y的one-hot表示
    for i in range(0, rate_levels - 1):  # 初始化b
        b[i] = i
    for n in range(0, N):  # 初始化 s
        for l in range(0, rate_levels - 1):
            if (y[n] <= l):
                s[n][l] = -1
            else:
                s[n][l] = 1
    last_err_ratio = 1.0 + delta
    for it in range(0, epochs):
        err_cnt = 0
        for n in range(0, N):
            E = np.zeros(rate_levels - 1) - 1  # 用于记录该样本
            for l in range(0, rate_levels - 1):
                if (s[n][l] * (np.dot(theta, X[n]) - b[l])) <= 0:
                    E[l] = l
            if(len(E[E >= 0]) > 0):
                err_cnt += 1
                sumval = 0  # 预测rate和真正rate 的间距，真正label是3，预测label是1，则sumval=3-1=2
                for l in range(0, rate_levels - 1):  # 统计 sumval
                    if(E[l] >= 0):
                        sumval += s[n][int(E[l])]
                for d in range(0, D):  # 更新theta
                    theta[d] += sumval * X[n][d]
                for l in range(0, rate_levels - 1):  # 更新b
                    if(E[l] >= 0):
                        b[int(E[l])] -= s[n][int(E[l])]
        cur_err_ratio = err_cnt * 1.0 / N
        print(err_cnt, N, cur_err_ratio)
        if abs(last_err_ratio - cur_err_ratio) < delta:
            break
        last_err_ratio = cur_err_ratio
    return theta, b

sklearn estimator版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
import numpy as np

from sklearn.base import TransformerMixin
from sklearn.base import BaseEstimator

class PRank(BaseEstimator, TransformerMixin):

    def __init__(self, rate_levels, epochs, delta):
        self._rate_levels =  rate_levels
        self._epochs = epochs
        self._delta = delta

    def _prank(self, X, y, rate_levels, epochs=10, delta=0.01):
        '''
        epochs: int, 收敛之前 遍历样本次数
        rate_lavels: int, y中rate级别的数量，如y用 0,1,2,3 标记，则rate_lavels = 4
        X: array 训练样本feature集合
        y: list 训练样本的rate集合，需要从 0开始。如为5级标注，需要为 0, 1, 2, 3, 4
        delta: float, 终止迭代条件
        '''
        N = len(X)  # 样本量
        D = len(X[0])  # 样本维度
        theta = np.zeros(D)
        b = np.zeros(rate_levels - 1)
        s = np.zeros((N, rate_levels - 1))  # 辅助变量，类似于y的one-hot表示
        for i in range(0, rate_levels - 1):  # 初始化b
            b[i] = i
        for n in range(0, N):  # 初始化 s
            for l in range(0, rate_levels - 1):
                if (y[n] <= l):
                    s[n][l] = -1
                else:
                    s[n][l] = 1
        last_err_ratio = 1.0 + delta
        for it in range(0, epochs):
            err_cnt = 0
            for n in range(0, N):
                E = np.zeros(rate_levels - 1) - 1  # 用于记录该样本
                for l in range(0, rate_levels - 1):
                    if (s[n][l] * (np.dot(theta, X[n]) - b[l])) <= 0:
                        E[l] = l
                if(len(E[E >= 0]) > 0):
                    err_cnt += 1
                    sumval = 0  # 预测rate和真正rate 的间距，真正label是3，预测label是1，则sumval=3-2=1
                    for l in range(0, rate_levels - 1):  # 统计 sumval
                        if(E[l] >= 0):
                            sumval += s[n][int(E[l])]
                    for d in range(0, D):  # 更新theta
                        theta[d] += sumval * X[n][d]
                    for l in range(0, rate_levels - 1):  # 更新b
                        if(E[l] >= 0):
                            b[int(E[l])] -= s[n][int(E[l])]
            cur_err_ratio = err_cnt * 1.0 / N
            # print(err_cnt, N, cur_err_ratio)
            if abs(last_err_ratio - cur_err_ratio) < delta:
                break
            last_err_ratio = cur_err_ratio
        return theta, b

    def fit(self, X, y):
        self.theta_, self.b_ = self._prank(X, y, self._rate_levels, self._epochs, self._delta)
        return self

    def predict(self, X):
        def get_rank(row):
            rank = len(row)
            for ind in range(len(row)):
                if row[ind] < 0:
                    rank = ind
                    break
            return rank
        scores = np.dot(X_test_scale, pranker.theta_)[:, np.newaxis] - pranker.b_ 
        pred = np.apply_along_axis(get_rank, 1, scores)
        return pred
    
    def score():
        pass

参考资料

Pranking with Ranking