偏度和峰度都是统计量
偏度Skewness(三阶) :三阶中心距除以标准差的三次方。描述分布偏离对称性程度的一个特征数。
峰度Kurtosis (四阶) :四阶中心矩除以标准差的平方 减去三。 用来反映频数分布曲线顶端尖峭或扁平程度的指标。
skew
是研究数据分布对称的统计量。通过对偏度系数的测量,我们能够判定数据分布的不对称程度以及方向。
具体来说,对于随机变量X,我们定义偏度为其的三阶标准中心矩:
$$
\mathrm{Skew}(\mathbf{X}) = E[(\frac{\mathbf{X}-\mu}{\sigma})^3] = \frac{E[(\mathbf{X}-\mu)^3]}{(E[(\mathbf{X}-\mu)^2])^{3/2}}=\frac{k_3}{k_2^{3/2}}
$$
其中: $\mu$为随机变量均值,$\sigma$为随机变量标准差
而对于样本的偏度,我们一般简记为SK,我们可以基于矩估计,得到有:
$$
\mathrm{SK} =\frac{m_3}{m_2^{3/2}} = \frac{\frac{1}{n}\sum(x_i-\bar x)^3}{[\frac{1}{n}\sum(x_i-\bar x)^2]^{3/2}}
$$
其中: $\bar x$为样本均值,$m_3$为样本三阶中心矩,$m_2$为样本的二阶中心矩。样本偏度的计算结果都属于有偏估计。
偏度的衡量是相对于正态分布来说,正态分布的偏度为0。因此我们说,若数据分布是对称的,偏度为0。
若偏度>0,则可认为高峰在左,分布为右偏,即分布有一条长尾在右;
若偏度<0,则可认为高峰在右,分布为左偏,即分布有一条长尾在左。
若偏度 = 0 - mean = median, the distribution is symmetrical around the mean.
同时偏度的绝对值越大,说明分布的偏移程度越严重。


Kurtosis
峰度,Kurtosis,是研究数据分布陡峭或平滑的统计量,通过对峰度系数的测量,我们能够判定数据分布相对于正态分布而言是更陡峭(peakedness)还是平缓(flattening)。
对于随机变量X,我们定峰度为其的四阶标准中心矩:
$$
\mathrm{Kurtosis}(\mathbf{X}) = E[(\frac{\mathbf{X}-\mu}{\sigma})^4] = \frac{E[(\mathbf{X}-\mu)^4]}{(E[(\mathbf{X}-\mu)^2])^{2}}
$$
此时正太分布的峰度系数是3,但是为了比较起来方便,很多软件(spss,python中的pandas工具)将峰度系数减去3,即使用如下公式计算。对于样本的峰度,我们一般简记为K,可通过如下公式计算样本的峰度系数:
$$
\mathrm{K} =\frac{m_4}{m_2^{2}} - 3 = \frac{\frac{1}{n}\sum(x_i-\bar x)^4}{[\frac{1}{n}\sum(x_i-\bar x)^2]^{2}} -3
$$
上式的分子分母都不是无偏估计量。
- Kurtosis > 3: Leptokurtic distribution, sharper than a normal distribution, with values concentrated around the mean and longer tails.This means high probability for extreme values.
- Kurtosis < 3: Platykurtic distribution, flatter than a normal distribution with a wider peak. The probability for extreme values is less than for a normal distribution, and the values are wider spread around the mean.
- Kurtosis = 3: Mesokurtic distribution - normal distribution for example.
峰度其实是一个相对于正态分布的对比量,正态分布的峰度系数为3,但是为了比较起来方便,很多软件(spss,python中的pandas工具)将峰度系数减去3,此时正态分布峰度值定为0。而均匀分布的峰度为-1.2,指数分布的峰度为6。
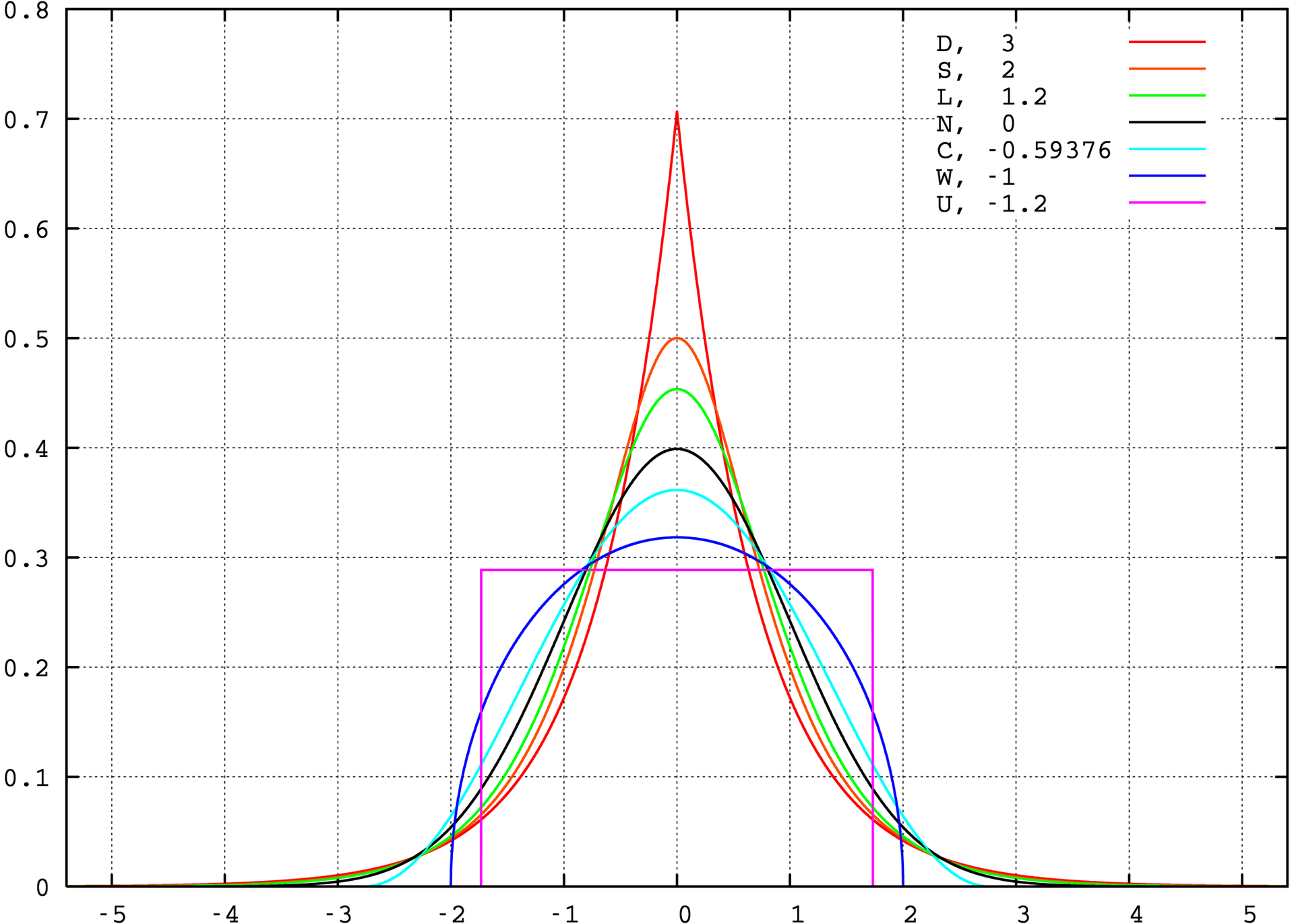
常见分布的 skewness 和 kurtosis 值见下表
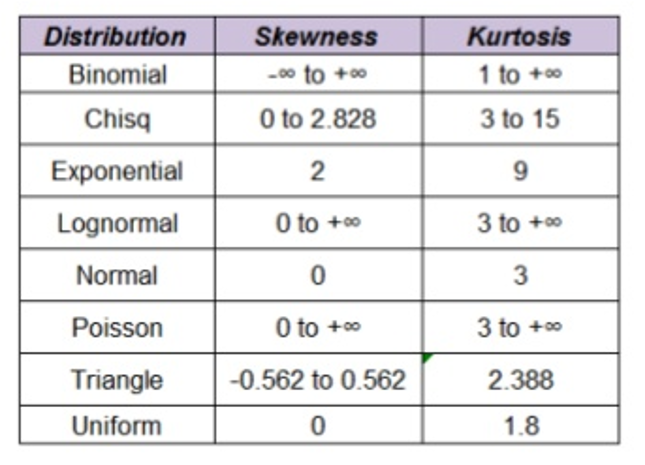
note:此表中列出的 kurtosis 是未减去 3 的版本。