举例

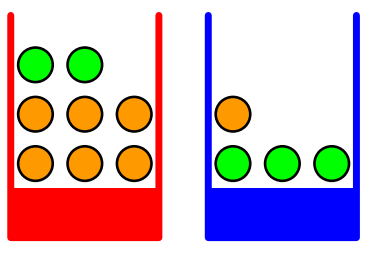
假设我们有两个盒子，一个红色的，一个蓝色的，红盒子中有2个苹果和6个橘子，蓝盒子中有3个苹果和1个橘子。现在假定我们随机选择一个盒子，从这个盒子中我们随机选择一个水果，观察选择了哪种水果，然后放回盒子中。我们重复这个过程很多次。

在这个例子中，我们要选择的盒子的颜色是一个随机变量，这个随机变量可以取两个值中的一个，即r(红盒子)或b(蓝盒子)。类似地，水果的种类也是一个随机变量，它可以取a（苹果）或者o（橘子）。

推导

这个例子涉及到两个随机变量$X$和$Y$ (如盒子的颜色和水果的种类)。我们假设$X$可以取任意的$x_i$ ，其中$i = 1,\dots, M$ ，并且$Y$ 可以取任意的$y_j$ ，其中$j = 1,\dots,L$。考虑一共进行$N$ 次试验，其中我们对$X$和$Y $都进行取样，把$X = x_i$ 且$Y = y_j$ 的试验的数量记作$n_{ij}$ 。并且，把$X$取值$x_i$（与$Y$ 的取值无关）的试验的数量记作$c_i$ ，把$Y $取值$y_j$ 的试验的数量记作$r_j$ 。

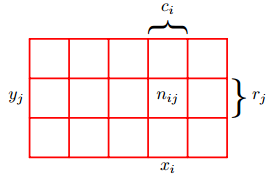
对于两个随机变量$X$和$Y$，$X$可能的取值为$\{x_1, \dots, x_M \}$， $Y$可能取值为$\{x_1, \dots, x_L \}$。

那么 $X=x_i, Y=y_j$ 的联合概率为:
$$
p(X=x_i, Y=y_j)=\frac{n_{ij}}{N}
$$
那么 $X=x_i$ 的概率为:
$$
p(X=x_i)=\frac{c_i}{N} = \sum_{j=1}^L p(X=x_i, Y=y_j)
$$
这是概率的加和规则（sum rule）。$p(X=x_i)$也被称为边缘概率(marginal probability)，因为它通过把其他变量（本例中的Y ）边缘化或者加和得到。

给定$X = x_i$ ，$Y = y_j$ 的条件概率（conditional probability）：
$$
p(Y = y_j | X = x_i)=\frac{n_{ij}}{c_i}
$$
那么：
$$
p(X=x_i, Y=y_j)=\frac{n_{ij}}{N} = \frac{n_{ij}}{c_i}\cdot \frac{c_i}{N} = p(Y = y_j | X = x_i)p(X=x_i)
$$
这被称为概率的乘积规则（product rule）。

总结

sum rule, 其实就是全概率公式
$$
p(X)= \sum_{Y} p(X, Y)
$$
product rule, 其实就是条件概率
$$
p(X,Y)=p(Y|X)p(X)
$$

参考资料

Pattern Recognition and Machine Learning