最近看书的过程中遇到了几次需要用到KKT条件的地方,每次都要重新翻书。本文单独将这一块的知识点拉出来做一下笔记,备查。
note : 本文中的所有向量默认都是列向量
概述
Lagrange multiplier和KKT都是用来解决非线性规划问题的。非线性规划的数学模型如下:
$$
\left \{
\begin {aligned}
\min & f(x) \\
s.t. & h_i(x) = 0 (i=1,2,\dots ,m) \\
& g_i(x) \ge 0 (i=1,2,\dots ,l) \\
\end {aligned}
\right .
$$
可以看出在这个问题中存在两种约束:等式约束和不等式约束 。把满足所有约束条件的点称做可行点 ( 可行解 ) , 所有可行点的集合称做可行域。
- 拉格朗日乘数法(Lagrange multiplier)是用于解决只含等式约束的非线性规划问题的。
- KKT条件是用于解决包含不等式约束问题的。
其中等式约束可以使用不等式约束等价表示:
$$
h_i(x) = 0 \iff
\left \{
\begin {aligned}
h_i(x) \ge 0 \\
-h_i(x) \ge 0 \\
\end {aligned}
\right .
$$
因而 , 也可将非线性规划的数学模型写成以下形式:
$$
\left \{
\begin {aligned}
\min & f(x) \\
s.t. & g_i(x) \ge 0 (i=1,2,\dots ,l) \\
\end {aligned}
\right .
$$
Lagrange multiplier
拉格朗日算子(Lagrange multiplier)在高等数学中有比较详细的讲解,本文先简要的记录一下。拉格朗日算子是用来解决具有等式约束的极值问题的,如:
$$
\left \{
\begin {aligned}
\min & f(x) \\
s.t. & h_i(x) = 0 (i=1,2,\dots ,m)\\
\end {aligned}
\right .
$$
即在$m$个等式约束下寻找能够使$f(x)$最小化的$x$ 。上式也可以写成向量形式:
$$
\left \{
\begin {aligned}
\min & f(x) \\
s.t. & H(x) = 0 \\
\end {aligned}
\right .
$$
其中:
$$
H(x) =
\begin{Bmatrix}
h_1(x) \\
h_2(x) \\
\vdots \\
h_m(x) \\
\end{Bmatrix}
=\begin{Bmatrix}
0 \\
0 \\
\vdots \\
0 \\
\end{Bmatrix}
$$
求解这个等式约束的最优化问题的步骤如下:
第一步:构建拉格朗日函数,将求$f(x)$最小值转变为求拉格朗日函数的最小值$L(x, \lambda)$
$$
L(x, \lambda) = f(x) - \lambda^{\mathrm T} H(x)
$$
第二步:假设点$\hat x$能够使 f(x) 在满足约束的条件下取的最小值,那么在该点处满足拉格朗日函数的 一阶必要条件。即,对$L(x, \lambda)$关于$x$和$\lambda$求偏导数,并令其为0
$$
\left \{
\begin {aligned}
\nabla_x f(\hat x) - J_H (\hat x) \lambda = 0 \\
H(\hat x) = 0 \\
\end {aligned}
\right . \tag1
$$
其中$ J_H (x)$是等式约束的雅克比矩阵,它的每一行表示一个等式约束关于$x$的梯度。
$$
J_H (x) =
\begin {Bmatrix}
(\nabla_x h_1(x))^{\mathrm{T}} \\
(\nabla_x h_2(x))^{\mathrm{T}} \\
\vdots \\
(\nabla_x h_m(x))^{\mathrm{T}} \\
\end {Bmatrix}
$$
通过求解(1)式得到能够使$f(x)$最小化的$\hat x$ ,和$f(x)$的最小值。
通过上式可以看出在极小值点处 $\nabla_x f(x) = J_H (x) \lambda$ ,即,该点处函数$f(x)$的梯度可以用所有等式约束的梯度向量线性表示。 (这句话是为了和KKT条件问题的论述相对应。)
下面以两种情况对该结论做以说明:
- 如果等式约束只有一个:如
$$
\left \{
\begin {aligned}
\min & f(x) \\
s.t. & h_1(x) = 0 \\
\end {aligned}
\right .
$$
则可以得到其拉个朗日函数的一阶条件如下:
$$
\left \{
\begin {aligned}
\nabla_x f(\hat x) - \lambda \nabla_x h_1(\hat x) = 0 \\
h_1(\hat x) = 0 \\
\end {aligned}
\right .
$$
此时极值点处函数$f(x)$的梯度和等式约束$h_1(x)$的梯度方向相同。
- 如果等式约束有两个:如
$$
\left \{
\begin {aligned}
\min & f(x) \\
s.t. & h_1(x) = 0 \\
& h_2(x) = 0 \\
\end {aligned}
\right .
$$
则可以得到其拉个朗日函数的一阶条件如下:
$$
\left \{
\begin {aligned}
\nabla_x f(\hat x) - \lambda_1 \nabla_x h_1(\hat x) - \lambda_2 \nabla_x h_2(\hat x) & = 0 \\
h_1(\hat x) & = 0 \\
h_2(\hat x) & = 0 \\
\end {aligned}
\right .
$$
此时极值点处函数$f(x)$的梯度可以用等式约束$h_1(x)$与$h_2(x)$的梯度向量线性表示。
KKT
在数学中,KKT条件是:
- 一个非线性规划问题有最优化解的一个一阶必要条件。
- 一个广义化拉格朗日乘数法。
- 用于解决包含不等式约束的最优化问题。
存在这样一个非线性规划问题:
$$
\left \{
\begin {aligned}
\min & f(x) \\
s.t. & g_i(x) \ge 0 (i=1,2,\dots ,l) \\
\end {aligned}
\right . \tag 2
$$
假定$\hat x$是非线性规划的极小点,该点可能位于可行域的内部,也可能处于可行域的边界上。
若为前者,这事实上是个无约束优化问题, 最优点 $\hat x$必满足条件 $\nabla_x f(\hat x) = 0$ ;
若为后者,情况就复杂得多了,现在我们来讨论后一种情形。
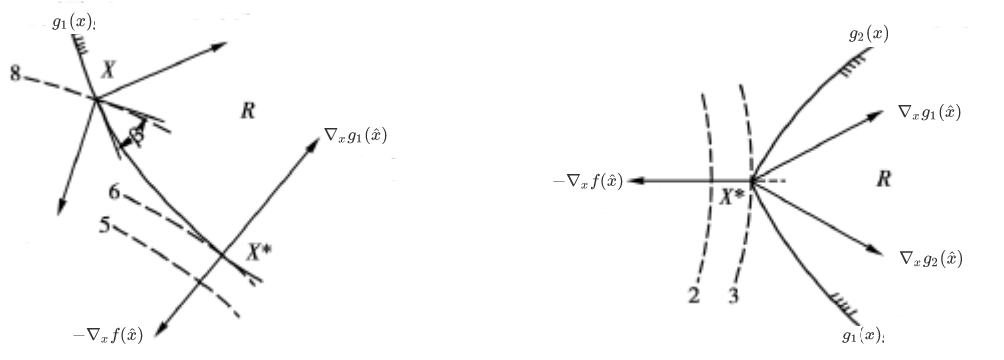
设最优点为$\hat x$。我们先讨论两个比较简单的特殊情况:$\hat x$落在一个不等式约束的边界上;$\hat x$处在两个不等式约束的共同作用下。
- 当$\hat x$落在一个不等式约束的边界上,即$\hat x$只处在一个不等式约束的作用下,假设这个不等式约束就是$g_1(x) \ge 0$ ,此时最优点$\hat x$必定落在函数$g_1(x) = 0$ 上。此时可以将问题转化为等式约束的非线性优化问题。
$$
\left \{
\begin {aligned}
\min & f(x) \\
s.t. & g_1(x) = 0 \\
\end {aligned}
\right .
$$
则可以得到其拉个朗日函数的 一阶必要条件 如下:
$$
\left \{
\begin {aligned}
\nabla_x f(\hat x) - \lambda_1 \nabla_x g_1(\hat x) & = 0 \\
g_1(\hat x) & = 0 \\
\end {aligned}
\right .
$$
如右图所示,虚线为$f(x)$的等值线,实线为约束函数$g_1(x)=0$ ,可行域在约束函数右侧。由于最优点$\hat x$在可行域的边界上,此时在点$\hat x$处没有可行下降方向,所以$\nabla_x g_1(\hat x)$必与$- \nabla_x f(\hat x)$在一条直线上且方向相反。结合上式可知此时 $\lambda_1 \ge 0$ ,所以:
$$
\left \{
\begin {aligned}
\nabla_x f(\hat x) - \lambda_1 \nabla_x g_1(\hat x) & = 0 \\
g_1(\hat x) & = 0 \\
\lambda_1 & \ge 0 \\
\end {aligned}
\right .
$$
- 若$\hat x$点有两个起作用约束 ,例如有 $g_1 (\hat x) = 0$ 和 $g_2 (\hat x) = 0$。此时可以将问题转化为等式约束的非线性优化问题。
$$
\left \{
\begin {aligned}
\min & f(x) \\
s.t. & g_1(x) = 0 \\
& g_2(x) = 0 \\
\end {aligned}
\right .
$$
则可以得到其拉个朗日函数的一阶条件如下:
$$
\left \{
\begin {aligned}
\nabla_x f(\hat x) - \lambda_1 \nabla_x h_1(\hat x) - \lambda_2 \nabla_x h_2(\hat x) & = 0 \\
g_1(\hat x) & = 0 \\
g_2(\hat x) & = 0 \\
\end {aligned}
\right .
$$
如左图所示,虚线为$f(x)$的等值线,实线为约束函数$g_1(x)=0$ 和$g_2(x)=0$,可行域在约束函数右侧。由于最优点$\hat x$在由$g_1(x)=0$ 和$g_2(x)=0$共同围成的边界上,所以$- \nabla_x f(\hat x)$与$\nabla_x g_1(\hat x)$的夹角必定大约90度,也就是说$\nabla_x f(\hat x)$必定处在$\nabla_x g_1(\hat x)$与$\nabla_x g_2(\hat x)$组成的夹角之内。结合上式可知此时 $\lambda_1 \ge 0 , \lambda_1 \ge 0$ ,所以:
$$
\left \{
\begin {aligned}
\nabla_x f(\hat x) - \lambda_1 \nabla_x h_1(\hat x) - \lambda_2 \nabla_x h_2(\hat x) & = 0 \\
g_1(\hat x) & = 0 \\
g_2(\hat x) & = 0 \\
\lambda_1 \ge 0 , \lambda_2 & \ge 0 \\
\end {aligned}
\right .
$$
若$\hat x$点有K个起作用约束($0 \le K \le l$) ,此时
$$
\left \{
\begin {aligned}
\nabla_x f(\hat x) - \sum_k^K \lambda_k \nabla_x g_k(\hat x) &= 0 \\
g_k(\hat x) &= 0, (k = 1,2 \dots K)\\
\lambda_k & \ge 0, (k = 1,2 \dots K)\\
\end {aligned}
\right .
$$
以上条件只是针对最优点$\hat x$处于可行域的边界上论述的,还有一种情况就是最优点处在可行域内部。将两种情况(最优点处在可行域内部和边界上)合并起来表示如下:
$$
\left \{\begin {aligned} \nabla_x f(\hat x) - \sum_i^l \lambda_i \nabla_x g_i(\hat x) &= 0 \\
g_i(\hat x) &\ge 0, (i = 1,2 \dots l) \\
\lambda_i g_i(\hat x) &= 0, (i = 1,2 \dots l) \\
\lambda_i & \ge 0, (i = 1,2 \dots l) \
\end {aligned}\right .
$$
可以看出当 $g_i(\hat x) = 0$ 时,它可能是对于最优点$\hat x$起作用的约束 , $\lambda_i$可以不为零;当$g_i(\hat x) \ne 0$ 时,即$g_i(\hat x) \gt 0$ ,此时它一定不是对最优点$\hat x$起作用的约束,此时必有$\lambda_i = 0$ 。
现可将库恩 - 塔克条件叙述如下 :设 $\hat x$ 是非线性规划式(2)的极小点 , 而且在 $\hat x$ 点的各起作用约束的梯度线性无关,则存在向量 $\Lambda = (\lambda_1 ,\lambda_2, \dots, \lambda_l)$ , 使下述条件成立 :
$$
\left \{
\begin {aligned}
\nabla_x f(\hat x) - \sum_i^l \lambda_i \nabla_x g_i(\hat x) &= 0 \\
g_i(\hat x) &\ge 0, (i = 1,2 \dots l) \\
\lambda_i g_i(\hat x) &= 0, (i = 1,2 \dots l) \\
\lambda_i & \ge 0, (i = 1,2 \dots l) \\
\end {aligned}
\right .
$$
库恩-塔克条件是非线性规划领域中最重要的理论成果之一,是确定某点为最优点的必要条件。但一般来说它并不是充分条件,因而满足这个条件的点不一定就是最优点。
对于凸规划问题,KKT条件既是最优点存在的必要条件,同时也是充分条件。
KKT条件总结
如本开头部分所述,含有不等式约束的非线性优化问题可以有多种表述,本节直接列出各种该表述的和其对饮高的KKT条件。
$$
\left \{
\begin {aligned}
& \min f(x) \\
s.t. & g_i(x) \ge 0 (i=1,2,\dots ,l) \\
\end {aligned}
\right .
\Rightarrow
\left \{
\begin {aligned}
\nabla_x f(\hat x) - \sum_i^l \lambda_i \nabla_x g_i(\hat x) &= 0 \\
g_i(\hat x) &\ge 0, (i = 1,2 \dots l) \\
\lambda_i g_i(\hat x) &= 0, (i = 1,2 \dots l) \\
\lambda_i & \ge 0, (i = 1,2 \dots l) \\
\end {aligned}
\right .
$$
$$
\left \{
\begin {aligned}
& \min f(x) \\
s.t. & g_i(x) \le 0 (i=1,2,\dots ,l) \\
\end {aligned}
\right .
\Rightarrow
\left \{
\begin {aligned}
\nabla_x f(\hat x) + \sum_i^l \lambda_i \nabla_x g_i(\hat x) &= 0 \\
g_i(\hat x) &\le 0, (i = 1,2 \dots l) \\
\lambda_i g_i(\hat x) &= 0, (i = 1,2 \dots l) \\
\lambda_i & \ge 0, (i = 1,2 \dots l) \\
\end {aligned}
\right .
$$
$$
\left \{
\begin {aligned}
& \min f(x) \\
s.t. & h_j(x) = 0 (j=1,2,\dots ,m) \\
& g_i(x) \ge 0 (i=1,2,\dots ,l) \\
\end {aligned}
\right .
\Rightarrow
\left \{
\begin {aligned}
\nabla_x f(\hat x) - \sum_j^m \gamma_j \nabla_x h_j(\hat x) - \sum_i^l \lambda_i \nabla_x g_i(\hat x) &= 0 \\
h_j(\hat x) &= 0 (j=1,2,\dots ,m) \\
g_i(\hat x) &\ge 0, (i = 1,2 \dots l) \\
\lambda_i g_i(\hat x) &= 0, (i = 1,2 \dots l) \\
\lambda_i & \ge 0, (i = 1,2 \dots l) \\
\end {aligned}
\right .
$$
$$
\left \{
\begin {aligned}
& \min f(x) \\
s.t. & h_j(x) = 0 (j=1,2,\dots ,m) \\
& g_i(x) \le 0 (i=1,2,\dots ,l) \\
\end {aligned}
\right .
\Rightarrow
\left \{
\begin {aligned}
\nabla_x f(\hat x) + \sum_j^m \gamma_j \nabla_x h_j(\hat x) + \sum_i^l \lambda_i \nabla_x g_i(\hat x) &= 0 \\
h_j(\hat x) &= 0 (j=1,2,\dots ,m) \\
g_i(\hat x) &\le 0, (i = 1,2 \dots l) \\
\lambda_i g_i(\hat x) &= 0, (i = 1,2 \dots l) \\
\lambda_i & \ge 0, (i = 1,2 \dots l) \\
\end {aligned}
\right .
$$
先列出这四种表述。
参考资料
运筹学-第三版