动态规划 - LIS and LCS

Posted on | In

最长上升子序列（LIS）

给定一个长度为n的整数序列A[]，求它的一个子序列(子序列即在原序列任意位置删除0或多个元素后的序列)，满足如下条件：

  1. 该序列单调递增；
  2. 在所有满足条件1的序列中长度是最长的。

让我们举个例子：求 2 7 1 5 6 4 3 8 9 的最长上升子序列。我们定义d[i]来表示前i个数以A[i]结尾的最长上升子序列长度。

  • d[1]=1 子序列为2；
  • d[2]=d[1]+1=2 子序列为2 7
  • d[3]=1 子序列为1
  • d[4]=d[1]+1=2 子序列为2 5
  • d[5]=d[4]+1=3 子序列为2 5 6
  • d[6]=d[1]+1=2 子序列为2 4
  • d[7]=d[1]+1=2 子序列为2 3
  • d[8]=d[5]+1=4 子序列为2 5 6 8
  • d[9]=d[8]+1=5 子序列为2 5 6 8 9

可以总结出递推公式为：
$$
d[i]=\max\{d[1],d[2],……,d[i-1]\} + 1
$$
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
using namespace std;

int LIS(int A[], int n) {
    int* d = new int[n];
    int len = 1;
    int i, j;
    for (i = 0; i < n; i++) {
        d[i] = 1;
        for (j = 0; j < i; j++) {
            if (A[j] <= A[i] && (d[j] + 1) >= d[i]) d[i] = d[j] + 1;
        }   
        if (d[i] > len) len = d[i];
    }   
    delete[] d;
    return len;
}

int main() {
    int A[9] = {2,7,1,5,6,4,3,8,9};
    cout << LIS(A, 9) << endl;
    return 0;
}

最长公共子序列(LCS)问题

在两个字符串中，有些字符会一样，可以形成的子序列也有可能相等，因此，长度最长的相等子序列便是两者间的最长公共字序列，其长度可以使用动态规划来求。

以s1={1,3,4,5,6,7,7,8},s2={3,5,7,4,8,6,7,8,2}为例。

借用《算法导论》中的推导图：

创建 DP数组C[][];

图中的空白格子需要填上相应的数字（这个数字就是 c[i, j] 的定义，记录的LCS的长度值）。填的规则依据递归公式，简单来说：如果横竖 (i, j)对应的两个元素相等，该格子的值 = c[i-1,j-1] + 1。如果不等，取c[i-1,j] 和 c[i,j-1]的最大值。首先初始化该表：

然后，一行一行地从上往下填：

S1的元素3 与 S2的元素3 相等，所以 c[2,1] = c[1,0] + 1。继续填充：

S1的元素3 与 S2的元素5 不等，c[2,2] =max(c[1,2],c[2,1])，图中c[1,2] 和 c[2,1] 背景色为浅黄色。

继续填充：

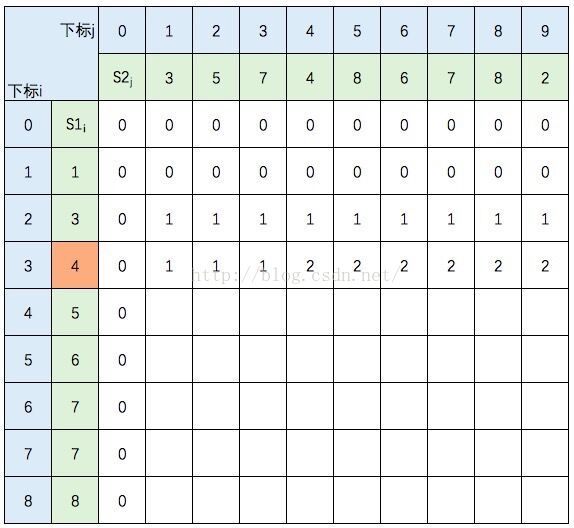
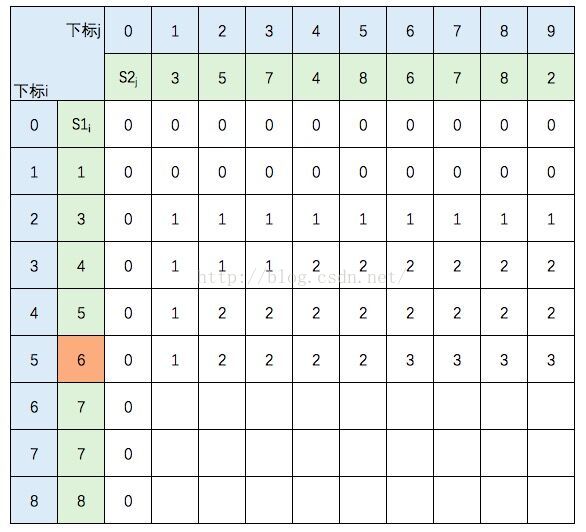
中间几行填写规则不变，直接跳到最后一行：

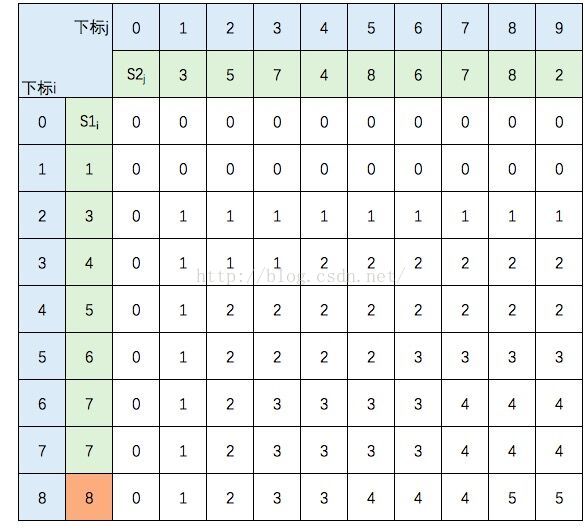
至此，该表填完。根据性质，c[8,9] = S1 和 S2 的 LCS的长度，即为5。

得到公式

$$
c[i,j]=
\left \{
\begin {align}
&0; & i=0 or j = 0 \\
&c[i-1, j -1] + 1; & i, j \gt 0 and x_i == y_j \\
&max\{C[i, j-1], C[i-1, j]\}; & i,j \gt0,x_i \ne y_i
\end {align}
\right .
$$

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include<string>
using namespace std;

int lcs(string str1, string str2) {
    int len1 = str1.length();
    int len2 = str2.length();
    int c[1000][1000]; // 此处假设字符串的最大长度为1000
    std::cout<< len1 << len2<<  endl;
    for (int i = 0; i <= len1; i++) {
        for( int j = 0; j <= len2; j++) {
            std::cout<< i << j << endl; 
            if(i == 0 || j == 0) {
                c[i][j] = 0;
                std::cout<< i << j << endl;
            } else if (str1[i-1] == str2[j-1]) {
                c[i][j] = c[i-1][j-1] + 1;
            } else {
                c[i][j] = max(c[i - 1][j], c[i][j - 1]);
            }   
        }   
    }   
    int result = c[len1][len2];
    return result;
}   

int main() {
    string str1 = "13456778";
    string str2 = "357486782";
    cout << lcs(str1, str2) << endl;
    return 0;
}
// 5

参考资料

动态规划：最长上升子序列（LIS）

LCS（最长公共子序列）