最近看了一些动态规划方面的东西，在此作一些笔记。

引例

动态规划算法的核心是记住已经求过的解，记住这些解的方式有两种：自顶向下和自底向上。其中自顶向下的方法也称为 备忘录法 。
【例1】为了说明动态规划的这两种方法，先举一个最简单的例子：求斐波拉契数列Fibonacci 。
$$
Fibonacci(n) =
\left \{
\begin {align}
& 0, n=0 \\
& 1, n=1 \\
& Fibonacci(n-1) + Fibonacci(n-2)
\end {align}
\right.
$$

通过递归方法很容易实现，代码如下：

#include <iostream>
using namespace std;

int fib_recursive(int n) { 
  if (n <= 0) return 0;
  if (n == 1) return 1;
  return fib_recursive(n - 1) + fib_recursive(n - 2);
}

int main() { 
  cout << fib_recursive(6) << endl;
  return 0;
}
// output 8

用下图表示上面的递归计算，每个节点代表依次计算。

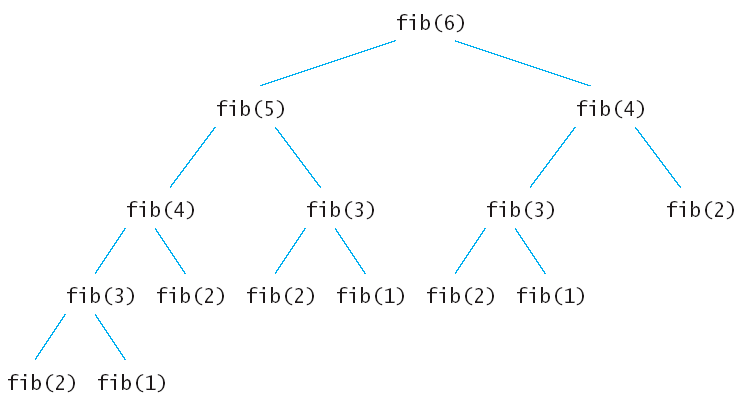
可以发现 fib(3) 和fib(4) 被分别重复计算了 3 次和 2次。也就是说有很多子节点被重复执行了，存在多余的计算。所以说这个问题还能有更优的求解方法。动态规划就是其优化方法，下面分别使用自顶向下的备忘录法和自底向上的两个方法求解。

备忘录法：

#include <iostream>
using namespace std;

int fib_memo(int n, int* Memo) { 
    if (Memo[n] != -1) return Memo[n];
    if (n == 0)
        Memo[n] = 0;
    else if (n == 1)
        Memo[n] = 1;
    else
        Memo[n] = fib_memo(n - 1, Memo) + fib_memo(n - 2, Memo);
    return Memo[n]; 
}   

int fib_memo_main(int n) { 
    int* Memo = new int[n + 1];
    for (int i = 0; i <= n; i++) Memo[i] = -1;
    int res = fib_memo(n, Memo);
    delete[] Memo;
    return res;
} 

int main() {
    cout << fib_memo_main(6) << endl;
    return 0;
}  
// output 8

备忘录法也是比较好理解的，创建了一个n+1大小的数组来保存求出的斐波拉契数列中的每一个值，在递归的时候如果发现前面fib(n)的值计算出来了就不再计算，如果未计算出来，则计算出来后保存在Memo数组中，下次在调用fib(n)的时候就不会重新递归了。比如上面的递归树中在计算fib(6)的时候先计算fib(5)，调用fib(5)算出了fib(4)后，fib(6)再调用fib(4)就不会在递归fib(4)的子树了，因为fib(4)的值已经保存在Memo[4]中。

自底向上：

备忘录法还是利用了递归，上面算法不管怎样，计算fib(6)的时候最后还是要计算出fib(1)，fib(2)，fib(3)……,那么何不先计算出fib(1)，fib(2)，fib(3)……,呢？这也就是动态规划的核心，先计算子问题，再由子问题计算父问题。

# 方法 1
#include <iostream>
using namespace std;

int fib_up1(int n) {
    int* Memo = new int[n + 1];
    Memo[0] = 0;
    Memo[1] = 1;
    for (int i = 2; i <= n; i++) { 
        Memo[i] = Memo[i - 1] + Memo[i - 2];
    } 
    int result = Memo[n];
    delete[] Memo;
    return result;
}

int main() { 
    cout << fib_up1(6) << endl;
    return 0;
} 
// output 8

自底向上方法也是利用数组保存了先计算的值，为后面的调用服务。观察参与循环的只有 i, i-1, i-2三项，因此该方法的空间复杂度可以进一步的压缩如下。

# 方法 2
#include <iostream>
using namespace std;

int fib_up2(int n) {
  if (n == 0) return 0; 
  if (n == 1) return 1;
  int Memo_i_2 = 0;
  int Memo_i_1 = 1;
  int Memo_i = 1; 
  for (int i = 2; i <= n; i++) {
    Memo_i = Memo_i_2 + Memo_i_1;
    Memo_i_2 = Memo_i_1;
    Memo_i_1 = Memo_i;
  }
  return Memo_i;
} 

int main() {
  cout << fib_up2(6) << endl;
  return 0;
}
// output 8

一般来说由于备忘录方式的动态规划方法使用了递归，递归的时候会产生额外的开销，使用自底向上的动态规划方法要比备忘录方法好。

适用的情况

能采用动态规划求解的问题的一般要具有2个性质：

最优子结构：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。因此，某个问题是否适合应用动态规划算法，它是否具有最优子结构性质是一个很好的线索。使用动态规划算法时，用子问题的最优解来构造原问题的最优解。
具有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）。在斐波拉契数列中，可以看到大量的重叠子问题，比如说在求fib(6)的时候，fib(2)被调用了5次。如果递归算法反复求解相同的子问题，就称为具有重叠子问题（overlapping subproblems）性质。在动态规划算法中使用数组来保存子问题的解，这样子问题多次求解的时候可以直接查表不用调用函数递归。
无后效性：如果给定某一阶段的状态，则在这一阶段以后过程的发展不受这阶段以前各段状态的影响。要求出fib(6)，只需要知道fib(5),fib(4)的值，而fib(5),fib(4)是如何算出来的，对fib(6)的求解释没有影响的。“未来与过去无关”，这就是无后效性。

核心思想

钞票问题

【例2】先来看看生活中经常遇到的事。假设您是个土豪，身上带了足够的1、5、10、20、50、100元面值的钞票。现在您的目标是凑出某个金额w，需要用到尽量少的钞票。

依据生活经验，我们显然可以采取这样的策略：能用100的就尽量用100的，否则尽量用50的……依次类推。在这种策略下，666=6×100+1×50+1×10+1×5+1×1，共使用了10张钞票。

这种策略称为“贪心”：假设我们面对的局面是“需要凑出w”，贪心策略会尽快让w变得更小。能让w少100就尽量让它少100，这样我们接下来面对的局面就是凑出w-100。长期的生活经验表明，贪心策略是正确的。

但是，如果我们换一组钞票的面值，贪心策略就也许不成立了。如果一个奇葩国家的钞票面额分别是1、5、11，那么我们在凑出15的时候，贪心策略会出错：

15=1×11+4×1 （贪心策略使用了5张钞票）
15=3×5 （正确的策略，只用3张钞票）

我们用f(n)来表示“凑出n所需的最少钞票数量”

$f(n)$ 只与 $f(n-1),f(n-5),f(n-11)$相关；更确切地说：

$$
f(n)=\min\{f(n-1),f(n-5),f(n-11)\}+1
$$

我们要求出f(n)，只需要求出几个更小的f值。利用自底向上的动态规划方法其代码如下：

#include <iostream>
using namespace std;

int bank_note(int n) {
    int* memo = new int[n + 1];
    memo[0] = 0;
    for (int i = 1; i <= n; i++) {
        int cost = n + 1;
        if (i - 1 >= 0) cost = std::min(cost, memo[i - 1] + 1);
        if (i - 5 >= 0) cost = std::min(cost, memo[i - 5] + 1);
        if (i - 11 >= 0) cost = std::min(cost, memo[i - 11] + 1);
        memo[i] = cost;
    }
    int result = memo[n];
    delete[] memo;
    return result;
}

int main() {
    cout << bank_note(15) << endl;
    return 0;
}